[Codility] StoneWall

You are going to build a stone wall. The wall should be straight and N meters long, and its thickness should be constant; however, it should have different heights in different places. The height of the wall is specified by an array H of N positive integers. H[I] is the height of the wall from I to I+1 meters to the right of its left end. In particular, H[0] is the height of the wall's left end and H[N−1] is the height of the wall's right end.

The wall should be built of cuboid stone blocks (that is, all sides of such blocks are rectangular). Your task is to compute the minimum number of blocks needed to build the wall.

Write a function:

class Solution { public int solution(int[] H); }

that, given an array H of N positive integers specifying the height of the wall, returns the minimum number of blocks needed to build it.

For example, given array H containing N = 9 integers:

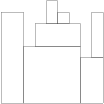
H[0] = 8 H[1] = 8 H[2] = 5 H[3] = 7 H[4] = 9 H[5] = 8 H[6] = 7 H[7] = 4 H[8] = 8

the function should return 7. The figure shows one possible arrangement of seven blocks.

Write an efficient algorithm for the following assumptions:

• N is an integer within the range [1..100,000];
• each element of array H is an integer within the range [1..1,000,000,000].

 

  이 문제의 핵심은 작은값들 중에 겹치는 값이 있으면 하나의 직사각형으로 묶여질 수 있다는 개념이다. 예제를 보게 되면 중간의 H[3] = H[6] = 7 이 겹쳐 하나로 묶이는 정보를 저장해놓고 있어야한다는 전제가 있어야한다. 따라서 Stack을 이용하여 index 마다의 높이값과 이전의 Stack 값들을 비교하여 H[i]가 Stack 값들보다 크면 Stack에 Push 하고 작을 경우 작은 값들을 Pop한다. 

이 문제를 풀때의 알고리즘은 기억해두면 비슷한 유형에서 이용하기 쉬울듯하다.

import java.util.*;

class Solution {
    public int solution(int[] H) {
        
        Stack<Integer> pastH = new Stack<>();
        
        int cnt = 0;
        
        for(int i : H){
            while(!pastH.empty() && i < pastH.peek()){
                pastH.pop();
            }
            
            if(pastH.empty() || i > pastH.peek()){
                pastH.push(i);
                cnt++;
            }
        }
        return cnt;
    }
}